School’s in session. Let’s talk about math.

Go back to your calculus class senior year in high school. You take the derivative of y with respect to x. You are finding the sensitivity to the change in the function with respect to a change in the argument. In practical terms, this is the slope of a line or the velocity of an object.

Then, take the derivative of the derivative—the second derivative. In practical terms, this measures the curvature of a line or the acceleration of an object. As it turns out, people have a very difficult time with the second derivative.

The second derivative is everywhere in finance. It is convexity in bonds or gamma in options. When someone blows up in the financial world, it is usually a failure to understand the second derivative. Human beings think linearly and statically. You may know your exposure here, but you may not know it over there.

Some second derivatives, like convexity and gamma, are measurable and known. Some of them are hidden and unknown. I’ve talked about hidden gamma before in The 10th Man, which we saw in March 2020—the point where people liquidate their positions and selling accelerates.

Once you see the second derivative, you can’t unsee it. It is everywhere you go. And then you’re on the lookout for it.

The second derivative produces charts like this:

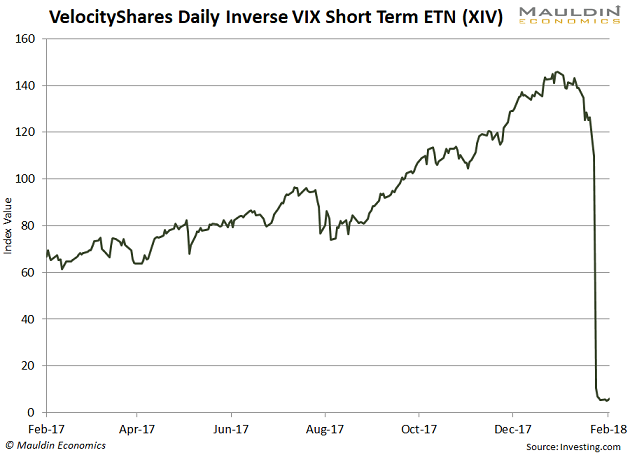
And then people wonder what the hell happened.

Stocks Have Convexity

The first thing to understand is that stocks have convexity. Some stocks are positively convex, and other stocks are negatively convex.

If that sounds like Greek to you, here’s a simpler way to think about it…

• A positively convex stock goes up faster than it comes down.

• A negatively convex stock goes down faster than it goes up.

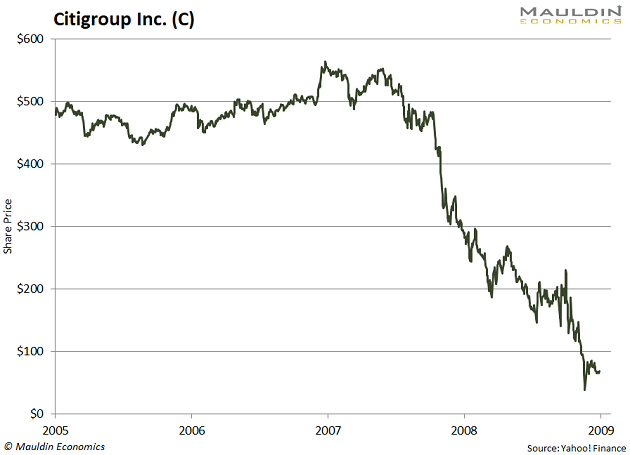
A lot of stocks, like the banks, were negatively convex in 2007. The banks had sold a great deal of optionality, which turned them into engines of negative convexity. They went up slowly and came down fast, which is roughly the payoff of a short option.

You can see this with Citigroup Inc. (C) in the next chart.

In general, tech stocks and biotech stocks are positively convex. But there are exceptions. And there are positively convex stocks in plenty of other industries, including retail, energy, and mining.

This doesn’t mean that you can’t have a negatively convex stock in your portfolio, but on balance, your portfolio should be positively convex. If bad things happen to the market, you want good things to happen to you.

A lot of people don’t realize that stocks have embedded convexity—they look at the chart and it seems pretty straightforward. Stocks go up and down. But sometimes they go up or down very rapidly.

Most of the analysis I do on stocks is not looking at static financial statements. It’s looking at how the underlying business can change in a convex fashion.

Convexity ends up fooling most people—they buy something that is linear that ends up being nonlinear in a malignant way. It’s a difficult concept to understand.

Many people dismiss the meme stocks like GameStop Corp. (GME) and AMC Entertainment Holdings, Inc., but there is a lot of convexity there, and gigantic opportunities. Convexity certainly fooled the people who were short GME.

Convexity is also created by liquidity, which is something I understand well, having worked on a program trading desk. If you own a stock that trades 500,000 shares a day, try to imagine what would happen if it traded 50,000,000 shares in a day. There is no place for it to go but up, or down.

Bonds

I had positions in preferred stock and high-yield bond funds up until recently. I sold them because of the massive negative convexity.

I try to keep things as simple as possible—high yield can’t go up much more, but it can go down a lot. One way to win, many ways to lose.

The coupon you get off high-yield bonds is like the premium you get from selling options. Sometimes (when the Fed isn’t involved), that premium is large and bonds become more attractive. People who understand income investing know intuitively about the negative convexity present in these strategies.

One of the tragedies of Zero Interest Rate Policy is that it has forced retirees to load up on negative convexity in search of income, usually in the form of corporate bonds and high dividend stocks.

In the old days, you could leave money in the bank, which was essentially zero convexity. If you look at a chart of the average retiree’s portfolio, it’s a series of slow climbs with breathtaking drops. The Federal Reserve, of all people, doesn’t understand convexity.

Once you start thinking about your portfolio in terms of convexity, your outcomes will improve. And I don’t mean just returns—I mean risk-adjusted returns.

Of course, the best way to add positive convexity to a portfolio is to just buy options. But for most people, that is better left to the experts.

One Last Thing

Don’t forget, The Daily Dirtnap summer party is in NYC on Friday, June 25. We only have about 10 tickets left—it’s going to sell out. If you’re thinking about going, I would scoop some up immediately here.

Jared Dillian

subscribers@mauldineconomics.com

• bonds
• convexity
• gamma
• optionality
• options